the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Satellite-based remote sensing data set of global surface water storage change from 1992 to 2018
Riccardo Tortini
Nina Noujdina
Samantha Yeo
Martina Ricko
Charon M. Birkett
Ankush Khandelwal
Vipin Kumar
Miriam E. Marlier
Dennis P. Lettenmaier
The recent availability of freely and openly available satellite remote sensing products has enabled the implementation of global surface water monitoring at a level not previously possible. Here we present a global set of satellite-derived time series of surface water storage variations for lakes and reservoirs for a period that covers the satellite altimetry era. Our goals are to promote the use of satellite-derived products for the study of large inland water bodies and to set the stage for the expected availability of products from the Surface Water and Ocean Topography (SWOT) mission, which will vastly expand the spatial coverage of such products, expected from 2021 on. Our general strategy is to estimate global surface water storage changes (ΔV) in large lakes and reservoirs using a combination of paired water surface elevation (WSE) and water surface area (WSA) extent products. Specifically, we use data produced by multiple satellite altimetry missions (TOPEX/Poseidon, Jason-1, Jason-2, Jason-3, and Envisat) from 1992 on, with surface extent estimated from Terra/Aqua Moderate Resolution Imaging Spectroradiometer (MODIS) from 2000 on. We leverage relationships between elevation and surface area (i.e., hypsometry) to produce estimates of ΔV even during periods when either of the variables was not available. This approach is successful provided that there are strong relationships between the two variables during an overlapping period. Our target is to produce time series of ΔV as well as of WSE and WSA for a set of 347 lakes and reservoirs globally for the 1992–2018 period. The data sets presented and their respective algorithm theoretical basis documents are publicly available and distributed via the Physical Oceanography Distributed Active Archive Center (PO DAAC; https://podaac.jpl.nasa.gov/, last access: 13 May 2020) of NASA's Jet Propulsion Laboratory. Specifically, the WSE data set is available at https://doi.org/10.5067/UCLRS-GREV2 (Birkett et al., 2019), the WSA data set is available at https://doi.org/10.5067/UCLRS-AREV2 (Khandelwal and Kumar, 2019), and the ΔV data set is available at https://doi.org/10.5067/UCLRS-STOV2 (Tortini et al., 2019). The records we describe represent the most complete global surface water time series available from the launch of TOPEX/Poseidon in 1992 (beginning of the satellite altimetry era) to the near present. The production of long-term, consistent, and calibrated records of surface water cycle variables such as in the data set presented here is of fundamental importance to baseline future SWOT products.
Information about surface water dynamics is required to support monitoring and reporting programs associated with water management as well as to support scientific objectives such as understanding the space–time variability in water stored at or near the land surface (Lettenmaier and Famiglietti, 2006). However, surface water storage data are scarce and often inaccessible in many regions of the world due to geographic remoteness and/or closed data policies in addition to the costs associated with maintaining extensive water monitoring programs. This is especially the case in areas with sparse populations and in the developing world, limiting our ability to understand the surface water balance at the global scale and therefore its effect on water management planning, global weather forecasting, ecosystem sustainability, and earth system modeling in general (Gao, 2015). The synoptic nature of satellite-based remote sensing platforms makes them ideally suited to quantitatively capture and portray conditions over large areas at a given point in time and to characterize how these conditions change through time over long periods (Lettenmaier et al., 2015; Crétaux et al., 2016; Zhang et al., 2017). With the recent availability of free and open-access satellite remote sensing products, users now have access to high-quality, analysis-ready imagery at spatial resolutions that are informative at the relevant scales about variation in water surface elevation (WSE) and water surface area (WSA), and ultimately storage, at least for relatively large inland water bodies. As a result, in recent years the hydrology community has been active in developing approaches to enable the implementation of global surface water monitoring strategies (McCabe et al., 2017). Global water dynamics studies that previously would have only been approachable with relatively low spatial resolution data sets or gravimetric remote sensing such as GRACE (e.g., Humphrey et al., 2016) are now implemented using high-resolution imagery such as Landsat. For example, the European Commission Joint Research Centre's Global Surface Water Explorer quantifies changes in global surface water at a 30 m resolution for a 32-year period (Pekel et al., 2016). In addition, despite being primarily designed to measure water levels over the open ocean, current-generation satellite altimetry missions have demonstrated their suitability for hydrological studies of large inland water bodies, both for specific targets such as Lake Chad (Coe and Birkett, 2004) and the Aral Sea (Aladin et al., 2005; Singh et al., 2012), and at the regional scale, for example the African Great Rift Valley lakes (Birkett et al., 1999) and the Tibetan Plateau (Lee et al., 2011; Zhang et al., 2011; Kleinherenbrink et al., 2015; Cai et al., 2016; Crétaux et al., 2016; Zhang et al., 2019). Extensive efforts have been made to measure surface height for large lakes and reservoirs globally; examples include the French Space Agency Laboratoire d'Etudes en Géophysique et Océanographie Spatiales Hydroweb database (LEGOS; Crétaux et al., 2011), the Database for Hydrological Time Series of Inland Waters (DAHITI; Schwatke et al., 2015), and the U.S. Department of Agriculture (USDA) Global Reservoirs and Lakes Monitor (G-REALM) data sets. Further examples of global data sets are the University of Stuttgart's HydroSat (http://hydrosat.gis.uni-stuttgart.de/; last access: 27 February 2020) and, despite being no longer actively maintained, the European Space Agency's River and Lake Altimetry products (http://altimetry.esa.int/riverlake; last access: 27 February 2020). However, surface water storage estimation at the global scale remains challenging and still largely unexplored (Gao et al., 2012; Gao, 2015). NASA's upcoming Surface Water and Ocean Topography (SWOT) mission (scheduled launch 2021) will fill a major void in the global observational capabilities of the hydrology community. SWOT is expected to produce accurate WSE and WSA estimates on average every 10.5 d (depending on specific location) with the ability to estimate surface water storage variations for lakes and reservoirs as small as about 1 km2 with a height accuracy of around 10 cm (Biancamaria et al., 2010). However, until SWOT data are available, the development of satellite-based long-term hydrological records for the study of variability and changes in the terrestrial water cycle will demand accurate data homogenization and harmonization from existing sensors, with transparent and reproducible methods playing a pivotal role in obtaining consistent and defensible results (McCabe et al., 2017). Moreover, given that the current generation of altimeters are nadir-pointing, i.e., they provide information along tracks rather than swaths (typically with track separation on the order of 100 km or so), long-term records can be obtained exclusively by merging data sets from a constellation of sensors with a range of (often overlapping) data records. For example, Crétaux et al. (2016) estimated that the constellation of Jason-2, Jason-3, the France–India SARAL AltiKa mission (Verron et al., 2015), and the European Space Agency's Sentinel-3 tandem (Donlon et al., 2012) has the potential to capture water surface elevation (WSE) for nearly the entirety of 3720 global lakes with areas larger than 50 km2 and 71 % of the 14 411 lakes larger than 10 km2, for a total of approximately 40 % of the global water storage of lakes on Earth.
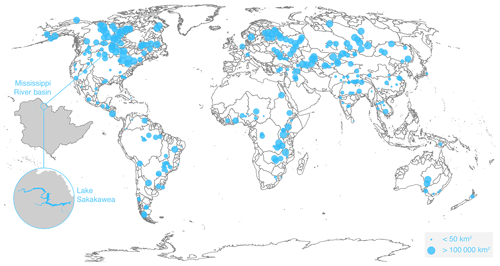
Figure 1Location of the global targets (blue bubbles, by average lake size) and Lake Sakakawea (approximate coordinates: 47.50∘ N, 101.41∘ W) within the Mississippi River basin (shaded).
However, this merging of records from heterogeneous satellite sources has practical drawbacks such as discontinuities in the derived water storage estimates, and the harmonization of these sources is fundamental to achieving more effective data assimilation for use in, for example, hydrological models, with the direct consequence of triggering a better understanding of any underlying physical process (McCabe et al., 2017). Here we summarize results of the integration of long-term satellite remote sensing data collected by optical and microwave sensors to produce global surface water storage records for large lakes and reservoirs, beginning with the launch of TOPEX/Poseidon (T/P) in 1992. We use data produced by multiple satellite altimetry missions, including but not limited to T/P, Jason-1, Jason-2, and Jason-3, with surface extent estimated from MODIS from 2000 on. We leverage the relationship between WSE and WSA (i.e., hypsometry) to produce estimates of storage changes (ΔV) even during periods when either of the variables is not available, as long as there are strong relationships between the two during an overlapping period. If the correlation coefficient between the two variables was smaller than 0.85 and the variance of either variable was smaller than 2 %, we simplified the model into a single variable (i.e., noninvariant) function. Our intent is to produce the most complete possible satellite-derived records of water ΔV over the period from the T/P launch up to the launch of the SWOT mission, with the goal of providing long-term, consistent, and calibrated records of baseline surface water cycle variables up to the time of the SWOT launch and beyond.
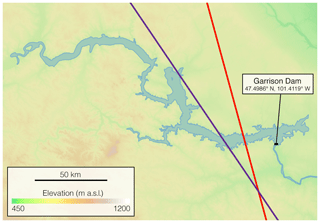
In this section, we describe the remote sensing data sources and the methods we used to estimate WSE, WSA, and ΔV. Given the technological limitations of the currently operational satellite platforms we used, we targeted water bodies globally with (i) WSE time series overlapping with WSA time series so that a hypsometric curve could be established for the 2000–2016 period, (ii) reference WSAs larger than 30 km2 (approximately 120 MODIS pixels with 500 m resolution), and (iii) lakes or reservoirs that were clearly distinguishable from other nearby water bodies (improved accuracy of both WSE and WSA estimates). As an example of the records we analyzed and their capabilities, we perform a detailed analysis of Lake Sakakawea (47.50∘ N, 101.41∘ W), a large reservoir located in the Missouri River basin in the Fort Berthold Indian Reservation in central North Dakota (USA) and impounded by the Garrison Dam. Figure 1 shows the location of the lakes and reservoirs selected for this work, with a close-up of Lake Sakakawea.
2.1 Water surface elevation
G-REALM10 merges T/P, Jason-1, Jason-2, and Jason-3 time series of relative WSE variations with respect to a given Jason-2 reference cycle at 10 d intervals (Birkett, 1995; Birkett and Beckley, 2010; Birkett et al., 2011), whereas, whenever 10 d measurements are not available, G-REALM35 is created using the Envisat time series of relative water level variations, for which the mean level of Envisat retrievals at 35 d intervals is the reference. ΔV monitoring of inland water bodies at the global scale has proved a challenging task (Gao et al., 2015; Crétaux et al., 2016), and the use of a single WSE data source significantly limits the creation of global ΔV data set. For these reasons, we used G-REALM10 as our primary elevation source for the creation of our global ΔV data set and, whenever G-REALM10 was not available for a specific target, supplemented it with LEGOS, DAHITI, and G-REALM35 (in this order) based on factors such as density and trend of the available measurements. Full details of the processing to create the G-REALM10 and G-REALM35 products can be found in the algorithm theoretical basis document (ATBD; Birkett et al., 2019). This includes the descriptions of the atmospheric corrections applied in the height reconstructions, the intermission height bias application, and the inherent differences between mission data set versions.
Figure 2 shows the radar altimeter ground tracks over Lake Sakakawea, where we merged multiple data sources to create the G-REALM10 and G-REALM35 records. We extracted WSE data for the portions of the ground tracks over the water body and used them to construct a time series of WSE variations. We used 10 d records from the TOPEX/Poseidon and Jason instrument series (1992–2002 and 2008–2017) with 35 d Envisat mission data used during the 2002–2008 period. A more detailed description of the methods we used can be found in Birkett (1995), Birkett and Beckley (2010), and Birkett et al. (2011). Ricko et al. (2012) performed both absolute and relative validations between the various G-REALM, DAHITI and LEGOS available product types and for the majority found an acceptable level of accuracy between them.
WSE accuracy is highly affected by the presence of ice, and for practical purposes, reliable ΔV estimates can only be produced under ice-free conditions. We assessed ice-on conditions (i.e., presence of snow-covered ice on the surface of a water body) using the MODIS Terra Snow Cover Daily Global product (Collection 5 MOD10A1). For each elevation record, we estimated lake ice phenology (i.e., ice-on and ice-off dates, defined as the beginning and end of the freezing period) as the proportion of frozen pixels identified in the NDSI-based 500 m spatial resolution Snow_Cover_Daily_Tile band (Hall and Riggs, 2007), and we determined a threshold for each water body as half of the maximum observed WSA. This algorithm uses the basic assumption that a water body, when deep and clear, absorbs the solar radiation incident upon it in almost its entirety. Whenever ice was identified, we created a flag that is provided as part of the ΔV records. Water bodies with high turbidity, algal blooms, or other conditions of relatively high reflectance from the water (e.g., salt crust) may be erroneously detected as snow and/or ice covered; in these cases we manually removed the ice flag. We classified data gaps within the freezing period as ice-on for continuity purposes. Additionally, we excluded observations during polar darkness because of a lack of complete data and likely ice-on conditions.
2.2 Surface water area
The Global Optical Lake Area (GOLA) determination process estimates the WSA of lakes and reservoirs from Terra/Aqua MODIS satellite optical imagery with a 500 m spatial resolution and an 8 d temporal resolution for the 2000–2016 period. In order to estimate the WSA of the target, a static spatial extent is required as one of the inputs (Khandelwal et al., 2017). We defined the initial spatial extents of water bodies using the vector polygons available as part of the Global Reservoir and Dam Database (GRanD; Lehner et al., 2011) and Global Lakes and Wetlands Database (GLWD; Lehner and Döll, 2004), with quality checks ensured by visual comparison with high-resolution satellite imagery (i.e., Google Earth, ESRI World Map). Whenever we identified a mismatch (i.e., polygon spatial extent not overlapping properly with the satellite imagery due to inaccurate georeferencing), the polygon was edited to match the expected location. In cases where a water body was not available as part of either database, a polygon was drawn by hand using high-resolution imagery from various sources (e.g., Global Surface Water Explorer, Google Earth, ESRI World Map). Once correctly identified, these locations were used to construct a mask for MODIS data extraction. We then used the mask to extract all of the data from three MODIS products whose nominal footprint overlapped the polygon of the corresponding lake. Specifically, we used (i) two multispectral reflectance data products from the MODIS instruments onboard NASA's Terra and Aqua satellites as an input to the water–land classification algorithm (Collection 5 MCD43A4 and MOD0911), and (ii) static water and land classification labels to train the classification model (MODIS MOD44W). The primary reflectance product was the bidirectional-reflectance-distribution-function-adjusted (BRDF-adjusted) MCD43A4 16 d composite product. The MCD43A4 product is generated by the U.S. Geological Survey (USGS) using data from both the Terra and Aqua satellites to assure that the combined data product is of the highest possible quality. However, by ignoring poor-data-quality pixels, the MCD43A4 product suffers from a high degree of missing values, especially before Aqua data became available in 2002. This can introduce a high degree of incompleteness in classification maps.
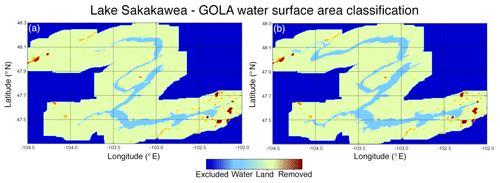
Figure 3Examples of the GOLA WSA classification results for Lake Sakakawea: (a) dry scenario (1 November 2008); (b) wet scenario (25 April 2011). Differences in WSA estimates are noticeable in the northwestern and southwestern branches of the reservoir, the farthermost from the Garrison Dam.
To alleviate this issue, we also used the MOD09A1 8 d composite product collected solely from the Terra satellite. Since the MOD09A1 product is generally less reliable than MCD43A4 as it is not BRDF-adjusted, we combined these two products to compensate for the primary limitations of each, in addition to compensating for noise and missing values following methods outlined by Khandelwal et al. (2017). We also used quality flags to filter out pixels with snow, ice, or clouds. For the MOD10A1 product, information about the data quality is available along with the multispectral values in the 16 bit quality assessment state flags, whereas the quality flags for the MCD43A4 product are available as a separate product (MCD43A2 BRDF/Albedo Quality product). In order to distinguish between land and water bodies, we used static water extent masks derived from the MODIS product (Carroll et al., 2009) to train the supervised classification models. This product, distributed publicly by the USGS, combines MODIS 250 m reflectance data with the SRTM Water Body Data from 60∘ N to 60∘ S, with reflectance data used solely poleward of 60∘ N. We aggregated the MOD44W product from 250 to 500 m to match the resolution of the other MODIS products. In particular, if the 500 m pixel had all of its four pixels at 250 m labeled as water or land in the MOD44W product, then we considered the pixel as a water or land pixel. We excluded partial pixels from the training set pool. Figure 3 shows an example of the classification results for Lake Sakakawea under a dry and a wet scenario. A more detailed description of the classification algorithm and its validation can be found in Khandelwal et al. (2017). All MODIS data used to create the GOLA records are publicly available via the USGS Land Processes Distributed Active Archive Center (LP DAAC; http://lpdaac.usgs.gov, last access: 13 May 2020).
2.3 Global storage change
During time periods when both WSEs from G-REALM (supplemented with DAHITI and LEGOS) and WSAs from GOLA were available, we derived the elevation–surface area relationships (i.e., hypsometry) for each target. We then used these relationships to estimate reservoir ΔV using an approach similar to that of Gao et al. (2012). Specifically, for overlapping G-REALM and GOLA periods, we calculated increments of volume for the corresponding changes in WSE and WSA as
where WSAt and WSEt are surface area and elevation at the smallest step t and At+1 and ht+1 are surface area and elevation at the next incremental step t+1.
We used linear regression to approximate the relationship between elevation (WSE) and surface area (WSA), WSA = f(WSE). We then applied this relationship to estimate WSA from WSE for periods when WSA is unavailable (1992–1999) and the inverse function WSE = f−1(WSA) to estimate WSE from WSA for periods when WSE is unavailable during the MODIS era (2017–2018). Finally, the ΔV equation can be simplified into a single variable function, as a function of either WSE or GOLA WSA, by substituting WSA = f(WSE) or WSE = f−1(WSA) into it. If the correlation coefficient between the two variables was smaller than 0.85 (i.e., weak to moderate correlation between WSE and WSA) and the variance of either variable was smaller than 2 % (i.e., near-invariant variable), then we parameterized the invariant variable using its mean value.
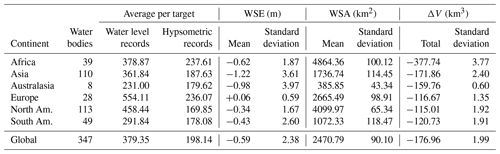
We created water storage records for 347 global lakes and reservoirs, distributed via the Physical Oceanography Distributed Active Archive Center (PO DAAC; https://podaac-tools.jpl.nasa.gov/drive/files/allData/preswot_hydrology/L3/lakes_reservoirs, last access: 13 May 2020) of NASA's Jet Propulsion Laboratory. Table 1 summarizes WSE, WSA, and ΔV per continent of the water bodies with records in the period of this work (i.e., 1992–2018). The majority of the water bodies (223, 64.26 % of the total) is located in Asia (110, of which 30 are in the Tibetan Plateau) and North America (113), with Australasia represented by just eight targets. Globally, approximately 22 % of the WSE measurements overlap with WSA records, enabling hypsometric curves to be constructed, with no significant regional exception. Africa and North America lead in terms of average WSA, with an average of ∼ 4864 km2 (39 water bodies) and ∼ 4100 km2 (113 water bodies), respectively. In fact, the dynamics of the water bodies in Africa are dominated by the Great Rift Valley lakes, whereas the size range of the water bodies in North America is more varied. South American water bodies instead show the highest variability (i.e., standard deviation) per average area (118.47 and 1072.33 km2, respectively), compatible with the generally modest topographic relief and frequent flooding of the major rivers and reservoirs. However, Africa also has the largest observed mean decrease in both ΔV (−377.74 km3) and standard deviation (3.77 km3), suggesting shallow topography and highly dynamic variations.
Figure 4 shows the monthly frequency of the observations used to create the hypsometric curve for the 347 targets we analyzed. The total number of hypsometric observations was 65 872 (average observations per target 189.83 or ∼ 11 per overlapping year). With the majority of the targets located in the Northern Hemisphere (272 targets, 78.4 % of the total), 55.86 % of the total hypsometric records are observed in the boreal late spring and summer months (May–September) and only 26.76 % in the boreal late fall and winter (November–March), due to a combination of factors such as fewer optical images with cloud cover, absence of ice cover, and in general more accurate WSE estimates.
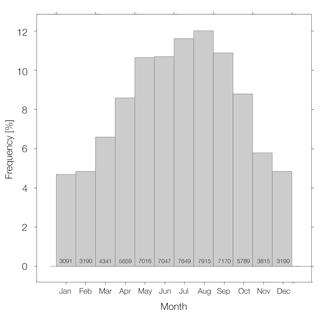
Figure 4Monthly frequency of the observations used to create the hypsometric curve for the 347 targets analyzed in this study, with total number of observations for each month.
Figure 5 shows the temporal trends of the observed G-REALM elevation and GOLA surface area records for Lake Sakakawea. Both data sets show consistent trends and seasonal variations for the overlapping period (2000–2016). The smoother seasonality associated with the GOLA records may be a direct consequence of the spectral heterogeneity associated with the low spatial resolution (i.e., 500 m) of the pixels along the target boundary. In addition, the sparser G-REALM35 records only partially compensate for the unavailability of G-REALM10 records from 2003 to 2008 (Fig. 5a). However, the denser GOLA time series in the same period (Fig. 5b) offers the potential to supplement further ΔV records based on the observed relationship with elevation records. This is especially relevant because the drainage area to Lake Sakakawea suffered a significant drought in the early 2000s. In fact, by May 2005 Lake Sakakawea had fallen to a documented all-time low of ∼ 550.4 m a.m.s.l. (1805.8 ft a.m.s.l.; US Army Corps of Engineers, 2007). However, thanks to a wet early summer in 2008 and the spring runoff of 2009, by 2010 Lake Sakakawea was nearly at full capacity. These dynamics are reflected in both the G-REALM and GOLA records (Fig. 5) and are consistent with the results obtained by Gao et al. (2012).
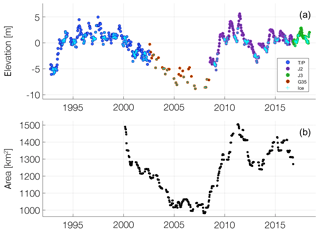
Figure 5Time series of (a) water elevation variation by mission (1144 records) and (b) MODIS-estimated surface area (578 records) for Lake Sakakawea. Presence of surface ice is indicated by a light blue cross.
Figure 6 shows the hypsometric curve for Lake Sakakawea (R2=0.908). Such a high correlation usually indicates good quality for both data sets; conversely, low correlations can result from many conditions. These include systematic errors in either water elevation or surface area records (or both) and/or in geomorphic properties of the target, with the possibility that, within the range of variation of either variable, the hypsometry is more or less independent of surface area (i.e., in the extreme vertical walls) or elevation (i.e., shallow lakes). Whenever direct observations of WSE were unavailable, we used the hypsometric curve to derive two associated products: inferred water elevation records and inferred surface area records.
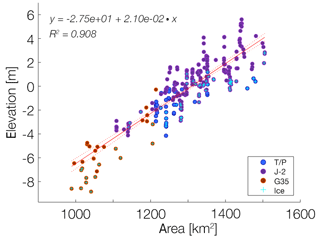
Figure 6Water elevation and surface area relationship for Lake Sakakawea (277 records). Presence of surface ice is indicated by a light blue cross.
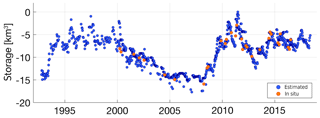
For the overlapping period (2000–2016) when both WSE and WSA were available, G-REALM was used in the final product to compute the relative storage because of its more relevant role played in the modeling of ΔV (cf. Eq. 1). Figure 7 shows the estimated relative storage time series for Lake Sakakawea.
We evaluated the statistical accuracy of WSE and storage estimates at Lake Sakakawea based on monthly in situ water measurements made by the U.S. Army Corps of Engineers at Garrison Dam (http://www.nwd-mr.usace.army.mil/rcc/projdata/garr.pdf, last access: 13 May 2020) and available from June 1967 to December 2018 (Fig. 8a, b). Specifically, we utilized the Average Daily Midnight Elevation (ft m.s.l.) and End-of-Month Storage (1000 AF) products. After averaging the WSE records to the monthly scale, 233 and 270 coincident observations were available for WSE and storage change, respectively.
The RMSE of the WSE was ∼ 0.68 m. The linear fit had an R2 of 0.95 (p<0.001), suggesting very good consistency between in situ water level measurements and the derived optical water levels (Fig. 8c). The RMSE of the storage change was 0.87 km3. The linear fit had an R2 of 0.94 (p<0.001), indicating very good consistency with the in situ storage estimates (Fig. 8d).

Figure 8Water levels and storage at Lake Sakakawea. (a) In situ monthly water levels (black) versus WSE records (red); (b) in situ monthly water storage (black) versus ΔV records (red); (c) linear regression of monthly average WSE records and concurrent in situ monthly water levels, with linear regression in red; (d) linear regression of monthly average ΔV records and concurrent in situ monthly water storage, with linear regression in red.
In the Lake Sakakawea example, both the G-REALM and GOLA records show consistent trends and seasonal variations for the overlapping period (2000–2016). Inaccuracy in the estimated relative storage can be attributed mainly to (i) WSE errors, (ii) WSA errors, and (iii) WSE–WSA relationship errors. The accuracy of the elevation records can be attributed to a number of factors, including satellite orbit, distance between antenna and target (i.e., altimetric range), geophysical range corrections, target size, and track location relative to the target boundary. Furthermore, each WSE record is calculated as the average value along the satellite ground track, with a large standard error implying higher uncertainty potentially from measurement errors and/or natural variations (e.g., surface roughness). For example, satellite tracks over narrow water bodies in complicated terrain will result in larger errors. Finally, major wind and precipitation events, as well as tidal effects and the presence of ice, also affect the quality of the records. The spectral heterogeneity associated with pixels along the target boundary plays a key role in the accuracy of the surface area classification. For example, Lake Sakakawea is a sinuous water body of 286 km length at capacity and with an average width of 3–5 km. As a result, a significant number of the MODIS 500 m pixels used to analyze the target are spectrally heterogeneous (i.e., partially covered by water and land) and therefore more prone to misclassification. This is especially true for droughts and/or periods of low water levels, as sinuous water bodies become even narrower due to drying. In addition, targets with limited or near-static water dynamics (defined as “dynamic region width” by Khandelwal et al., 2017) present land cover changes in the GOLA product primarily near the boundary of the static region used in the classification. Due to the moderate spatial resolution of the GOLA records, the effect of mixed pixels is even more prominent in water bodies with a low dynamic region width, which can lead to low correlation values between elevation and surface area. Conversely, the classification of targets with a high dynamic region width consistently performs better in the GOLA records. The quality of both elevation and surface area contribute to the accuracy of their relationship, but volume changes are mostly dominated by elevation changes. High correlations between elevation and area generally indicate reliable ΔV estimation. However, if either variable is systematically biased, the error associated with the relationship is carried to the estimated ΔV. For example, low correlation may arise when the target shows nearly constant WSA (vertical walls, in which case a variation in elevation is reflected in a negligible change in WSA) or nearly constant elevation (i.e., shallow lakes, in which case a variation in surface area is reflected in a negligible change in elevation). In these cases we proceeded in the modeling of ΔV with the parameterization of the invariant variable with its mean value. All the factors listed above introduce some degree of error in the WSE–WSA relationship; however, in most cases a linear approximation does not appear to be a major contributor (cf. Gao et al., 2012). At the global scale, the limited number of altimeter-based WSE products is a key constraint for satellite remote sensing observations. In fact, due to the technical limitations listed above, current-generation spaceborne microwave altimeters can only monitor WSEs for a relatively small number of large reservoirs when used individually. In order to maximize the length and density of global ΔV records, in addition to integrating measurements from multiple altimeters, multiple MODIS daily overpasses played a crucial role in creating consistent 8 d GOLA and consequently ΔV records.
Despite the GOLA product's moderate spatial resolution, it can potentially affect the accuracy of ΔV estimates; higher-resolution satellite missions have longer satellite revisit times (e.g., 16 d for Landsat, 10 d for Sentinel-2A starting in 2015, and 5 d for Sentinel-2A and -2B in tandem formation starting in 2017). Because we leveraged the relationship between WSE and WSA to estimate ΔV, such satellite revisit times would produce sparser records, especially for water bodies located at high latitudes and/or altitudes as they are more affected by cloud cover. In fact, despite being highly desirable for the monitoring of surface water dynamics, imagery from optical sensors is strongly affected by the presence of cloud cover, which can be extensive in late fall and winter, and in combination with low sun angles experienced at high latitudes this may limit its usefulness at the global scale (Duguay et al., 2014). However, the integration of optical imagery (e.g., MODIS, Landsat, Sentinel-2) and radar altimetry data provides long-term continuity in the production of consistent and calibrated records, and we encourage the re-exploration of the lakes in our study using Landsat and/or Sentinel images with a 20–30 m spatial resolution.
The data sets presented and their respective ATBDs are publicly available and distributed via the Physical Oceanography Distributed Active Archive Center (PO DAAC; https://podaac-tools.jpl.nasa.gov/drive/files/allData/preswot_hydrology/, last access: 13 May 2020) of NASA's Jet Propulsion Laboratory. Specifically, the WSE data set is available at https://doi.org/10.5067/UCLRS-GREV2 (Birkett et al., 2019), the WSA data set is available at https://doi.org/10.5067/UCLRS-AREV2 (Khandelwal and Kumar, 2019), and the ΔV data set is available at https://doi.org/10.5067/UCLRS-STOV2 (Tortini et al., 2019). The links listed provide the location of the data repositories, and they are all active and publicly accessible.
We generated global water storage change (ΔV) estimates based exclusively on satellite remote sensing observations through the creation of elevation-associated (i.e., G-REALM) and surface-area-associated (i.e., GOLA) products for 347 selected large water bodies, primarily based on the availability of water elevation products. G-REALM10 was derived from a constellation of satellite altimeters (i.e., TOPEX/Poseidon, Jason-1, Jason-2, Jason-3), whereas G-REALM35 was created using measurements from Envisat. We supplemented the G-REALM elevation records with DAHITI and LEGOS products. We utilized the algorithm developed by Khandelwal et al. (2017) to create 8 d 500 m surface area estimates from MODIS images. WSE and WSA were used to derive the hypsometric relationship for each reservoir, with either variable inferable from its counterpart when direct observations were unavailable. We computed ΔV using an adaptation of the method of Gao et al. (2012). As an example, we demonstrated the application of the data set to Lake Sakakawea (North Dakota, USA), the second largest reservoir in the USA by area and representative of the challenges encountered in the creation of global ΔV records. The records presented in this paper represent the most complete satellite-derived global surface water storage time series to date, spanning from 1992 (TOPEX/Poseidon launch) to the present, with the potential to be extended up to the launch of the SWOT mission planned for 2021. The data set presented is dynamic and will continue to be extended both in terms of the number of water bodies (with ultimate potential total around 400) and historical time period. Despite the coarser spatial resolution of the pre-SWOT records presented, the production of long-term, consistent, and calibrated records of surface water cycle variables is of fundamental importance to establishing a baseline of what is known globally about surface water ΔV up to the time of the SWOT launch.
All authors contributed to the research design. CB and MR created the WSE data set; AK and VP created the WSA data set; RT, NN, SY, and DL formatted the WSE and WSA data sets, modeled storage, and created the ΔV data set. RT wrote the manuscript with supervision from DL and contributions and approval from all coauthors.
The authors declare that they have no conflict of interest.
The data sets presented are available as additional material to this paper and distributed via NASA's PO DAAC (https://podaac-tools.jpl.nasa.gov/drive/files/allData/preswot_hydrology/, last access: 13 May 2020) as L2 (level variation), L3 (surface area), and L4 (storage change) products. We would like to thank Jessica Hausman (NASA JPL) for comments on the content and format of the records produced in this work and Jongyoun Kim for her work on earlier versions of the data set. We acknowledge that Lake Sakakawea lies on the traditional territory of the Mandan, Hidatsa, and Arikara, who still walk the land today.
This research has been supported by the NASA Making Earth System Data Records for Use in Research Environments (MEaSUREs) program (grant no. NNX13AK45A to UCLA) and the National Science Foundation (grant nos. 1029711 and 1838159 to UMN).
This paper was edited by David Carlson and reviewed by two anonymous referees.
Aladin, N., Crétaux, J. F., Plotnikov, I. S., Kouraev, A. V., Smurov, A. O., Cazenave, A., Egorov, A. N., and Papa, F.: Modern hydro‐biological state of the Small Aral sea, Envirometrics, 16, 375–392, https://doi.org/10.1002/env.709, 2005.
Biancamaria, S., Andreadis, K. M., Durand, M., Clark, E. A., Rodriguez, E., Mognard, N. M., Alsdorf, D. E., Lettenmaier, D. P., and Oudin, Y.: Preliminary characterization of SWOT hydrology error budget and global capabilities, IEEE J. Sel. Top Appl., 3, 6–19, https://doi.org/10.1109/JSTARS.2009.2034614, 2010.
Birkett, C. M.: The contribution of TOPEX/POSEIDON to the global monitoring of climatically sensitive lakes, J. Geophys. Res.-Atmos., 100, 25179–25204, https://doi.org/10.1029/95JC02125, 1995.
Birkett, C. M. and Beckley, B.: Investigating the performance of the Jason-2/OSTM radar altimeter over lakes and reservoirs, Mar. Geod., 33, 204–238, https://doi.org/10.1080/01490419.2010.488983, 2010.
Birkett, C. M., Murtugudde, R., and Allan, J. A.: Indian Ocean climate event brings floods to East Africa’s lakes and Sudd Marsh, Geophys. Res. Lett., 26, 1031–1034, https://doi.org/10.1029/1999GL900165, 1999.
Birkett, C. M., Reynolds, C., Beckley, B., and Doorn, B.: From Research to Operations, in: The USDA Global Reservoir and Lake Monitor, edites by: Vignudelli, S., Kostianoy, A. G., Cipollini, P., and Benveniste, J., Coastal Altimetry, Springer, Heidelberg, Germany, 19–50, ISBN 978-3-642-12796-0, 2011.
Birkett, C. M., Ricko, M., and Yang, X.: Pre SWOT Hydrology Global Lake/Reservoir Surface Inland Water Height GREALM V.2, Version 2, PO.DAAC, CA, USA, https://doi.org/10.5067/UCLRS-GREV2, 2019.
Cai, X., Feng, L., Hou, X., and Chen, X.: Remote Sensing of the Water Storage Dynamics of Large Lakes and Reservoirs in the Yangtze River Basin from 2000 to 2014, Sci. Reports, 6, 36405, https://doi.org/10.1038/srep36405, 2016.
Carroll, M. L., Townshend, J. R., DiMiceli, C. M., Noojipady, P., and Sohlberg, R. A.: A New Global Raster Water Mask at 250 m Resolution, Int. J. Digit. Earth, 2, 291–308, https://doi.org/10.1080/17538940902951401, 2009.
Coe, M. T. and Birkett, C. M.: Calculation of river discharge and prediction of lake height from satellite radar altimetry: example for the Lake Chad basin, Water Resour. Res., 40, W10205, https://doi.org/10.1029/2003WR002543, 2004.
Crétaux, J. F., Jelinski, W., Calmant, S., Kouraev, A., Vuglinski, V., Bergé-Nguyen, M., Gennero, M. C., Nino, F., Abarca Del Rio, R., Cazenave, A., and Maisongrande, P.: SOLS: a lake database to monitor in near real time water level and storage variations from remote sensing data, Adv. Space Res., 47, 1497–1507, https://doi.org/10.1016/j.asr.2011.01.004, 2011.
Crétaux, J. F., Abarca-del-Río, R., Bergé-Nguyen, M., Arsen, A., Drolon, V., Clos, G., and Maisongrande, P.: Lake Volume Monitoring from Space, Surv. Geophys., 37, 269–305, https://doi.org/10.1007/s10712-016-9362-6, 2016.
Donlon C., Berruti B., Buongiorno A., Ferreira M. H., Féménias P., Frerick J., Goryl P., Klein U., Laur, H., Mavrocordatos, C., Nieke, J., Rebhan, H., Seitz, B., Stroede, J., and Sciarra, R.: The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission, Remote Sens. Environ., 120, 37–57, https://doi.org/10.1016/j.rse.2011.07.024, 2012.
Duguay, C. R., Bernier, M., Gauthier, Y., and Kouraev, A.: Remote sensing of lake and river ice, in: Remote sensing of the cryosphere, edited by: Tedesco, M., John Wiley & Sons, Chichester, UK, 273–306, https://doi.org/10.1002/9781118368909.ch12, 2014.
Gao, H.: Satellite remote sensing of large lakes and reservoirs: from elevation and area to storage, WIREs Water, 2, 147–157, https://doi.org/10.1002/wat2.1065, 2015.
Gao, H., Birkett, C. M., and Lettenmaier, D. P.: Global monitoring of large reservoir storage from satellite remote sensing, Water Resour. Res., 48, W09504, https://doi.org/10.1029/2012WR012063, 2012.
Hall, D. K. and Riggs, G. A.: Accuracy assessment of the MODIS snow products, Hydrol. Process., 21, 1534–1547, https://doi.org/10.1002/hyp.6715, 2007.
Humphrey, V., Gudmundsson, L., and Seneviratne, S. I.: Assessing global water storage variability from GRACE: trends, seasonal cycle, subseasonal anomalies and extremes, Surv. Geophys., 37, 357–395, https://doi.org/10.1007/s10712-016-9367-1, 2016.
Khandelwal, A. and Kumar, V.: Pre SWOT Hydrology Global Lake/Reservoir Surface Inland Water Area Extent V2, Version 2, PO.DAAC, CA, USA, https://doi.org/10.5067/UCLRS-AREV2, 2019.
Khandelwal, A., Karpatne, A., Marlier, M. E., Kim, J., Lettenmaier, D. P., and Kumar, V.: An approach for global monitoring of surface water extent variations in reservoirs using MODIS data, Remote Sens. Environ., 202, 113–128, https://doi.org/10.1016/j.rse.2017.05.039, 2017.
Kleinherenbrink, M., Lindenbergh, R. C., and Ditmar P. G.: Monitoring of lake level changes on the Tibetan Plateau and Tian Shan by retracking Cryosat SARIn waveforms, J. Hydrol., 521, 119–131, https://doi.org/10.1016/j.jhydrol.2014.11.063, 2015.
Lee, H., Shum, C. K., Tseng, K. H., Guo, J. Y., and Kuo, C. Y.: Present-day lake level variation from Envisat altimetry over the northeastern Qinghai-Tibetan Plateau: links with precipitation and temperature, Terr. Atmos. Ocean. Sci., 22, 169–175, https://doi.org/10.3319/TAO.2010.08.09.01, 2011.
Lehner, B. and Döll, P.: Development and validation of a global database of lakes, reservoirs and wetlands, J. Hydrol., 296, 1–22, https://doi.org/10.1016/j.jhydrol.2004.03.028, 2004.
Lehner, B., Reidy Liermann, C., Revenga, C., Vörösmarty, C., Fekete, B., Crouzet, P., Döll, P., Endejan, M., Frenken, K., Magome, J., Nilsson, C., Robertson, J., Rödel, R., Sindorf, N., and Wisser, D.: High-resolution mapping of the world's reservoirs and dams for sustainable river-flow management, Front. Ecol. Environ., 9, 494–502, https://doi.org/10.1890/100125, 2011.
Lettenmaier, D. P. and Famiglietti, J. S.: Water from on high, Nature, 444, 562–563, https://doi.org/10.1038/444562a, 2006.
Lettenmaier, D. P., Alsdorf, D., Dozier, J., Huffman, G. J., Pan, M., and Wood, E. F.: Inroads of remote sensing into hydrologic science during the WRR era, Water Resour. Res., 51, 7309–7342, https://doi.org/10.1002/2015WR017616, 2015.
McCabe, M. F., Rodell, M., Alsdorf, D. E., Miralles, D. G., Uijlenhoet, R., Wagner, W., Lucieer, A., Houborg, R., Verhoest, N. E. C., Franz, T. E., Shi, J., Gao, H., and Wood, E. F.: The future of Earth observation in hydrology, Hydrol. Earth Syst. Sci., 21, 3879–3914, https://doi.org/10.5194/hess-21-3879-2017, 2017.
Pekel, J. F., Cottam, A., Gorelick, N., and Belward, A. S.: High-resolution mapping of global surface water and its long-term changes, Nature, 540, 418–422, https://doi.org/10.1038/nature20584, 2016.
Ricko, M., Birkett, C. M., Carton, J. A., and Crétaux, J. F.: Intercomparison and validation of continental water level products derived from satellite radar altimetry, J. Appl. Remote Sens., 6, 061710, https://doi.org/10.1117/1.JRS.6.061710, 2012.
Schwatke, C., Dettmering, D., Bosch, W., and Seitz, F.: DAHITI – an innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry, Hydrol. Earth Syst. Sci., 19, 4345–4364, https://doi.org/10.5194/hess-19-4345-2015, 2015.
Singh, A., Seitz, F., and Schwatke, C.: Inter-annual water storage changes in the Aral Sea from multi-mission satellite altimetry, optical remote sensing, and GRACE satellite gravimetry, Remote Sens. Environ., 123, 187–195, https://doi.org/10.1016/j.rse.2012.01.001, 2012.
Tortini, R., Noujdina, N., Yeo, S., Khandelwal, A., Kumar, V., Birkett, C. M., Ricko, M., Yang, X., and Lettenmaier, D. P.: Lake and Reservoir Storage Time Series V2, Version 2, PO.DAAC, CA, USA, https://doi.org/10.5067/UCLRS-STOV2, 2019.
US Army Corps of Engineers: Garrison Dam/Lake Sakakawea master plan with integrated programmatic environmental assessment: Missouri River, North Dakota: Update of design memorandum MGR-107D, 2007, available at: https://usace.contentdm.oclc.org/digital/collection/p16021coll7/id/91/rec/1, last access: 13 May 2020.
Verron, J., Sengenes, P., Lambin, J., Noubel, J., Steunou, N., Guillot, A., Picot, N., Coutin-Faye, S., Sharma, R., Gairola, R. M., Raghava Murthy, D. V. A., Richman, J. G., Griffin, D., Pascual, A., Rémy, F., and Gupta, P. K.: The SARAL/AltiKa Altimetry Satellite Mission, Mar. Geod., 38, 2–20, https://doi.org/10.1080/01490419.2014.1000471, 2015.
Zhang, G., Xie, H., Kang, S., Yi, D., and Ackley, S. F.: Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009), Remote Sens. Environ., 115, 1733–1742, https://doi.org/10.1016/j.rse.2011.03.005, 2011.
Zhang, G., Yao, T., Shum, C. K., Yi, S., Yang, K., Xie, H., Feng, W., Bolch, T., Wang, L., Behrangi, A., Zhang, H., Wang, W., Xiang, Y., and Yu, J.: Lake volume and groundwater storage variations in Tibetan Plateau's endorheic basin, Geophys. Res. Lett., 44, 5550–5560, https://doi.org/10.1002/2017GL073773, 2017.
Zhang, G., Chen, W., and Xie, H.: Tibetan Plateau's Lake Level and Volume Changes From NASA's ICESat/ICESat-2 and Landsat Missions, Geophys. Res. Lett., 46, 13107–13118, https://doi.org/10.1029/2019GL085032, 2019.