the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A review of biomass equations for China's tree species
Yunjian Luo
Xiaoke Wang
Zhiyun Ouyang
Fei Lu
Liguo Feng
Jun Tao
Tree biomass equations are the most commonly used method to estimate tree and forest biomasses at various spatial and temporal scales because of their high accuracy, efficiency and conciseness. For decades, many tree biomass equations have been reported in diverse types of literature (e.g., journals, books and reports). These scattered equations are being compiled, and tree biomass equation datasets are currently available for many geographical regions (e.g., Europe, North America and sub-Saharan Africa) and countries (e.g., Australia, Indonesia and Mexico). However, one important country stands out as an area where a large number of biomass equations have not yet been reviewed and inventoried extensively: China. Therefore, in this study, we carried out a broad survey and critical review of the literature (from 1978 to 2013) on biomass equations in China and compiled a normalized tree biomass equation dataset for China. This dataset consists of 5924 biomass equations for nearly 200 tree species and their associated background information (e.g., geographical location, climate and stand description), showing sound geographical, climatic and forest vegetation coverage across China. The dataset is freely available at https://doi.org/10.1594/PANGAEA.895244 (Luo et al., 2018) for noncommercial scientific applications, and this dataset fills an important regional gap in global biomass equations and provides key parameters for biomass estimation in forest inventory and carbon accounting studies in China.
Globally, forests are the dominant terrestrial ecosystem, occupying 30.6 % of the global land area (1.3×1010 ha) (FAO, 2016). An important challenge that has been faced by ecologists and foresters for decades is how to enhance the accuracy, consistency, and efficiency of forest biomass and carbon estimations at various spatial and temporal scales, which are essential to understanding forest carbon cycling and implementing forest carbon offset activities (Bustamante et al., 2014; Chave et al., 2014). However, current estimates still have considerable uncertainties (Pan et al., 2013), due in large part to the limited geographical coverage of the estimation methods and their related parameters. Tree biomass equations are commonly used for estimating forest biomass and carbon because of their high accuracy, efficiency and conciseness (Chave et al., 2014; Paul et al., 2016), but this method still faces a shortage of localized parameters.
Tree biomass equations refer to quantitative relationships between tree biomass (or tree components, such as stems, branches, leaves and roots) and one or more dendrometric variables (e.g., tree diameter and height). Since the International Biological Program, a large number of tree biomass equations have been developed for tree species and forest types at specific sites. These biomass equations, which were scattered in various literature (e.g., journals, reports and books), have been evaluated and inventoried for geographical regions such as Europe (Zianis et al., 2005; Forrester et al., 2017), Latin America (Návar, 2009), North America (Ter-Mikaelian and Korzukhin, 1997; Jenkins et al., 2004), Southeast Asia (Yuen et al., 2016), and sub-Saharan Africa (Henry et al., 2011) and for countries such as Australia (Eamus et al., 2000; Keith et al., 2000), Indonesia (Anitha et al., 2015) and Mexico (Rojas-García et al., 2015). As a global initiative, the international web platform GlobAllomeTree (http://www.globallometree.org/, last access: 1 November 2019), launched in 2013, further promotes the compilation of global biomass equations (Henry et al., 2015). This work is of great significance to goals such as (1) facilitating the identification of the gaps in the coverage of the equations, (2) testing and comparing existing equations with new ones, (3) developing generalized biomass equations (Forrester et al., 2017; Jenkins et al., 2003), (4) validating and calibrating process-based models and remotely sensed biomass estimates (Rojas-García et al., 2015) and integrating these models with remotely sensed data (e.g., tree height and crown breadth) (Jucker et al., 2017), and (5) elucidating and confirming the generality of plant allometric scaling laws (Návar, 2009; Pilli et al., 2006).
China covers most of the world's terrestrial biomes and environmental gradients and has a series of forest types ranging from tropical rainforest to boreal forest (Zhang, 2007). It is said that “if you study China, you'll know the world” (Fang et al., 2012). In the late 1970s, studies to measure tree biomass and develop biomass equations were initiated in China (Pan et al., 1978; Zhang and Feng, 1979). Subsequently, many studies have expanded to nearly all climatic zones and forest types in China (Luo et al., 2014). Some biomass equation datasets have been built for specific regions (e.g., northeastern China, Chen and Zhu, 1989; Xishuangbanna Forest Region and Hainan Island, Yuen et al., 2016), specific forest types (e.g., Cunninghamia lanceolata forest, Zhang et al., 2013; Larix forest, Wang et al., 2005; Populus forest, Liang et al., 2006) and short time periods (e.g., from 1978 to 1996, Feng et al., 1999). Currently, the platform GlobAllomeTree includes 1145 tree biomass equations from China, but they are very limited in scope, such as data sources (23 scientific articles), spatial coverage (39 sites) and tree species (ca. 50 species) (accessed on 1 November 2019). More importantly, these existing datasets employ different screening criteria for data inclusion. Therefore, tree biomass equations for China still have not been reviewed and inventoried extensively. In addition, China's biomass equations are currently of limited use to stakeholders worldwide because of restricted data accessibility in terms of the written language (Chinese) and hard copies (Cheng et al., 2014).
Here, after our Ecology data paper on forest biomass and its allocation (Luo et al., 2014; the related dataset is freely accessible at http://www.esapubs.org/archive/ecol/E095/177/, last access: 1 November 2019), we continued to review biomass equations for China's tree species from a broad literature survey and then developed a normalized tree biomass equation dataset (Luo et al., 2018). The dataset represents a major expansion relative to the biomass equation datasets currently available for China and fills an important regional gap in global biomass equations.
2.1 Literature retrieval
Concerning tree biomass equations in China (excluding Taiwan Province in our study), we made a great effort to collect the available literature (journals, books and reports) between 1978 and 2013. Using a series of keywords (biomass, allometry, allometric, relationship, equation, model and function) with logical operators, studies were retrieved from national libraries (National Digital Library of China and China Forestry Digital Library), online literature databases (Web of Science, China Knowledge Resource Integrated Database, and China Science and Technology Journal Database), reference lists from our Ecology data paper (Luo et al., 2014) and existing compilations of biomass equations (Feng et al., 1999; Wang et al., 2005; Liang et al., 2006; Xiang et al., 2011; Zhang et al., 2013). During the literature survey, no a priori criteria (e.g., tree species, tree age, site condition, measurement method and statistical technique) were applied.
2.2 Data collection
A critical review of the collected literature was conducted to obtain reliable biomass equations, using the following criteria.

Figure 1The division of tree components. A tree can be divided into (i) aboveground sector above the soil surface and (ii) belowground sector, which are often subdivided into finer components.
2.2.1 Scope
Equations for inclusion were restricted to those for both forest-grown trees and open-grown trees. However, equations for mangrove trees and recently disturbed trees (e.g., coppicing, pruning, fire and pest insects) were not included.
2.2.2 Measurement method
A robust measurement method should cover the appropriate survey period (during the growing season, especially for deciduous trees), plot setting and tree biomass (the oven-dried mass) measurements (see Feng et al., 1999). Generally, plot areas were not smaller than 100 m2 for boreal and temperate forests, 400 m2 for subtropical forests, and 1000 m2 for tropical forests. To develop biomass equations, at least three sample trees should be selected to determine tree biomass and its components (e.g., stem, branch, leaf and root) through destructive harvesting and weighing. The division of tree components can be summarized as shown in Fig. 1, although the number of tree components varied with the different purposes of the investigations.
-
Aboveground biomass. The biomass of at least three aboveground tree components (stem, branch, leaf or their whole subcomponents) should be determined. If any of the three components or their subcomponent biomass was not measured, the aboveground biomass and relevant biomass (e.g., tree crown) were considered to be inadequate.
-
Belowground biomass. The quality of total belowground biomass was evaluated from three aspects. (i) The total belowground biomass should be the total biomass of the entire root system (i.e., root crown and different root diameters), as determined by using either the full excavation method for the entire root system or a hybrid of the full excavation method for the root system (excluding fine roots) and the soil pit method (or soil coring method) for fine roots. (ii) The excavation area was larger than or equal to the average tree area covered, and the excavation depth reached the maximum depth where roots were nearly absent, which was more than at least 50 cm (Mokany et al., 2006). (iii) Fine roots are usually classified as roots with diameters of < 2–5 mm (Finér et al., 2011). Fine roots play significant roles in the water and nutrient uptake of trees but contribute little to the total belowground biomass (Mokany et al., 2006). However, if the minimum measured root diameter is > 5 mm, the total belowground biomass may be significantly underestimated.
2.2.3 Equation building
Biomass equations should be developed using robust regression methods (e.g., ordinary least squares, maximum likelihood and Bayesian techniques), explicit equation forms (e.g., power, exponential and linear equations) and valid equation evaluations.
-
Predictor variables. The predictor variables for the biomass equations were limited to the tree diameter at a certain height (e.g., basal diameter and diameter at breast height, i.e, 1.3 m above soil surface), tree height and a combination of both. These variables were used mostly because other variables (e.g., stand density, site index and soil type) were highly related to local conditions and thus reduced the robustness and generality of the biomass equations.
-
Equation forms. If two or more equation forms with the same predictor variable(s) were used to build the equations, the regression results of only one equation form were selected. More specifically, if the differences (< 0.05) in coefficients of determination (R2) or correlation coefficient (R) were small among all equation forms, the priority order of equation forms for inclusion was power, exponential and other (e.g., polynomial and hyperbolic); otherwise, the equation form with the highest R2 (or R) was selected. Moreover, for studies that had original data rather than equations, equations were fitted using this original data and two typical allometric models: and , where W is the biomass (kg), Dx is the tree diameter at x height (cm), H is the tree height (m), and a and b are equation coefficients.
-
Equation evaluation. The goodness-of-fit of regression equations should be evaluated, and the statistical measures R2 and R are commonly used in studies in China. Goodness-of-fit measures other than R2 and R were not included in our dataset, largely because diverse forms of the error estimates were employed in the different studies. In addition, several correction factors are proposed to correct the systematic bias in the biomass estimates by using log-linearized equations (Clifford et al., 2013); thus, they were collected for log-linearized equations if available.
Table 1Summary of variable information in the dataset, which is available at https://doi.org/10.1594/PANGAEA.895244 (Luo et al., 2018).
2.2.4 Quality checking
Robust measurement methods and reliable equation building methods should be adopted in the original studies. The biomass equations being considered for inclusion were checked and were even corrected using original biomass data if available. With increasing tree sizes (diameter and height), the biomass equations did not show unreasonable ranges of tree biomass or biomass allocations. Tree biomass and its allocations were regarded as acceptable if they fell within the biomass and allocation ranges of average trees by forest type and age class (Luo et al., 2013). When the biomass or biomass allocation of the trees that were generated by an equation were outside the abovementioned empirical ranges, the equation was considered questionable and then rechecked to evaluate its inclusion in our dataset.
Biomass equations that met the above criteria were compiled to develop China's dataset of tree biomass equations (Luo et al., 2018), mainly consisting of an equation sheet and a general sheet. The former sheet includes the tree species for which the biomass equations were developed, tree component, predictor variable, equation form, equation coefficients, goodness-of-fit statistics (e.g., correlation coefficient and coefficient of determination) and applicable ranges (i.e., determination methods and the value ranges of predictor variables). The latter sheet contains background information for the equations, including the geographical location (e.g., latitude, longitude and altitude), climate (mean annual temperature, MAT, and mean annual precipitation, MAP) and stand description (e.g., forest type, dominant species, stand origin, stand age and tree spacing). The detailed variables and their descriptions in the dataset are summarized in Table 1.
2.3 Estimation of missing data
Not all original studies reported the geographical location, climate data (MAT and MAP) or applicable ranges of the biomass equations. These missing data were estimated as follows.
-
Geographical location. Google Earth was used to estimate the geographical centers of the study sites in the original studies without geographical location descriptions in the form of latitude, longitude and altitude.
-
Climate data. The 30 arcsec (ca. 1 km at the Equator) resolution global climate database WorldClim version 1.4 (http://worldclim.org/current, last access: 1 November 2019) was generated through the interpolation of average monthly climatic records from the period 1950–2000 (Hijmans et al., 2005). This database has been shown to be highly accurate in estimating climate data (MAT and MAP) in China (Luo et al., 2014). Therefore, MAT and MAP data were extracted using geographic coordinates from WorldClim version 1.4 in this study.
-
Applicable ranges of biomass equations. Empirical biomass equations were built based on sample trees with limited ranges of tree size (diameter and height). When these equations are applied beyond the ranges for which they were developed, the reliability of the biomass estimates is often questionable (Henry et al., 2011). The size ranges of the sample trees were not always given in the original studies, and it was not possible to access the raw data used for equation building. According to the amount and reliability of the information in the original studies, five methods (Table 2) were used to obtain the applicable ranges for the biomass equations. However, some applicable ranges were finely calibrated under the rule “tree biomass increases with increasing tree size”.

Figure 2Spatial distribution of study sites: (a) geographical coverage and (b) climate space. Mean annual temperature and precipitation of sites are superimposed upon Whittaker's climate biome diagram (Whittaker, 1975).
Table 2Methods for determining applicable ranges of biomass equations*.

* According to the amount and reliability of information in the original studies, five methods are employed in priority order: I > II > III > IV > V. Concerning those biomass equations with diameter and height as predictor variables, when only diameter ranges are determined, height ranges are estimated from (i) biomass ranges or (ii) height–diameter relationships (height–diameter curves or height/diameter ratios). The biomass ranges are from original studies or are calculated by using diameter-based equations if equations based on both diameter and height are available. Height–diameter relationships are from original studies or are developed by using the raw data of diameter and height within original studies or using mean diameter and height data from Luo et al. (2013) (Appendix B).
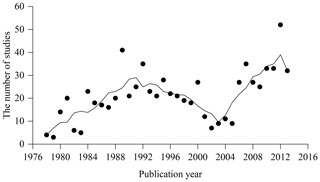
From 518 references (see full list in https://doi.org/10.1594/PANGAEA.895244, Luo et al., 2018) during the period 1978–2013, 759 studies and 5924 biomass equations from these studies were compiled in China's tree biomass equation dataset. Temporal changes in the number of studies showed a continuously increasing trend from 1978 to 1990, while a decreasing trend was found during the period 1991–2002 (Appendix C). Since 2002, there has been a generally increasing trend. Studies from 1978 to 1990, 1991 to 2002 and 2003 to 2013 contributed 27.4 %, 34.0 % and 38.6 % of the total studies, respectively. These studies were carried out in 359 sites, showing broad geographical coverage (18.6–52.4∘ latitude, 76.8–130.7∘ longitude and 2–4588 m in altitude) across China (Fig. 2a) and broad climatic ranges (−5.6–24.6 ∘C in MAT and 39–2500 mm in MAP), representing all biomes from desert to tropical rainforest (Fig. 2b).
These compiled studies and equations varied greatly with forest type, stand origin and tree species (Fig. 3; Appendix D). The studied forests were categorized into five types: deciduous coniferous forest, evergreen coniferous forest, deciduous broadleaved forest, evergreen broadleaved forest, and coniferous–broadleaved mixed forest. Among the five forest types, evergreen coniferous forest had the most studies and equations (45.7 % and 38.7 % of the total studies and equations, respectively), followed by deciduous broadleaved forest (22.9 % and 24.1 %), evergreen broadleaved forest (17.5 % and 21.0 %), deciduous coniferous forest (10.4 % and 9.5 %) and coniferous–broadleaved mixed forest (3.4 % and 6.7 %) (Fig. 3a). In terms of stand origins, 77.2 % and 68.8 % of the total studies and equations, respectively, focused on planted forests (Fig. 3b). Apart from mixed species, there were 5488 equations specific to 197 species (Appendix D). However, only 63 species were in more than two studies, occupying 80.5 % of the total species-specific equations. The five most commonly studied species were Cunninghamia lanceolata (n=130), Pinus massoniana (n=60), Pinus tabuliformis (n=46), Pinus koraiensis (n=32) and Larix principis-rupprechtii (n=30), which had 706, 365, 395, 218 and 235 equations, respectively.
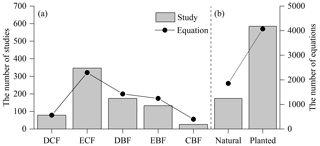
Figure 3Distribution of compiled studies and biomass equations by (a) forest type and (b) stand origin. Forests are categorized by forest type, i.e., deciduous coniferous forest (DCF), evergreen coniferous forest (ECF), deciduous broadleaved forest (DBF), evergreen broadleaved forest (EBF), and coniferous and broadleaved mixed forest (CBF), and by stand origin, i.e., natural forest and planted forest.
Compared with the aboveground sector, the belowground sector was not always measured. Many studies (n=177) did not (properly) address the belowground sector, accounting for 23.3 % of the total studies. Equations for stem biomass and its subcomponents accounted for 27.1 % of the total 5924 equations, while branch biomass and its subcomponents accounted for 20.1 %, leaf biomass and its subcomponents accounted for 19.3 %, aboveground biomass accounted for 6.1 %, belowground biomass and its subcomponents accounted for 18.3 %, and total tree biomass accounted for 7.8 % (Appendix D). However, only 1.2 % of the equations were for other biomass components, such as flower and fruit biomass and tree crown biomass.

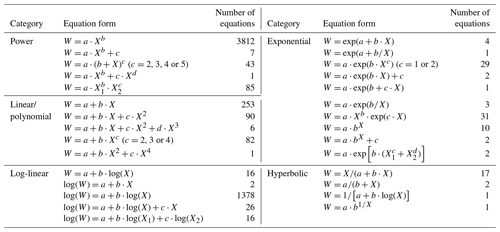
Figure 4Distribution of compiled biomass equations by (a) predictor variable and (b) equation form. D and H are diameter at breast height (1.3 m) and height, and Dc is tree diameter at heights (e.g., 0, 0.2 and 0.3 m) other than breast height. Equation forms used in original studies are categorized into power equation, log-linear equation, linear/polynomial equation, exponential equation and hyperbolic equation (Appendix E).
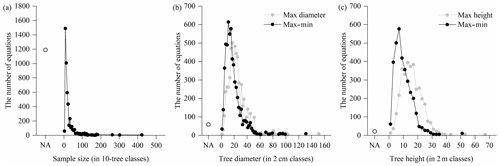
Figure 5Distribution of sample size and applicable range of compiled biomass equations: (a) sample size, (b) tree diameter and (c) tree height. Dots represent the number of equations within each class. If sample sizes and applicable ranges are not available, they are indicated by “NA”.
Of the 5924 equations, 43.5 % were based on a single predictor (diameter or height) and 56.5 % were based on two predictors (diameter and height) or a combination of both (Fig. 4a). The diameter at breast height was the most frequently used predictor in the biomass equations (96.8 %), whereas tree diameter at heights other than breast height was used in 185 equations (3.1 %). Moreover, only 9 equations (0.2 %) employed tree height as a single predictor. In total, 29 equation forms were applied to develop the quantitative relationships of tree biomass with tree diameter and/or height, which were categorized into five types: power equation, log-linear equation, linear/polynomial equation, exponential equation and hyperbolic equation (Appendix E). Power equations were the most frequently used type (3948 equations, accounting for 66.6 % of the equations), followed by the log-linear equations (1438, 24.3 %), linear/polynomial equations (432, 7.3 %), exponential equations (85, 1.4 %) and hyperbolic equations (21, 0.4 %) (Fig. 4b).
A considerable proportion (20.1 %) of the total 5924 equations did not specify the sample size (i.e., the number of trees harvested to develop the equations) (Fig. 5a). The sample size varied from 3 and 420 trees, where the most common sample sizes were between 6 and 25 trees, accounting for 74.5 % of the 4734 equations with specified sample sizes. For the applicable ranges of equations, 2790 out of the 5924 equations had clear applicable ranges in the original studies. There was a great bias towards the smaller diameter classes (Fig. 5b) and height classes (Fig. 5c). From the 5856 equations with available diameter ranges, the maximums and ranges (max–min) of tree diameter varied between 1.6 and 150.0 cm and between 1.0 and 130.0 cm, respectively, and 74.4 % and 86.2 % of the equations had maximums and ranges lower than 30 cm, respectively. From the 3336 equations with available height ranges, the maximums and ranges of the height ranged from 1.2 to 66.8 m and from 0.6 to 51.5 m, respectively, and most of them (73.7 % and 94.1 %) were lower than 20 m.
This version of China's tree biomass equation dataset was developed from studies that were published from 1978 to 2013. Data collection is ongoing, and the dataset will be updated as additional data are collected and verified. The dataset is freely available at https://doi.org/10.1594/PANGAEA.895244 (Luo et al., 2018) for noncommercial scientific applications, but the free availability of the dataset does not constitute permission to reproduce or publish it.
In this study, we developed a normalized tree biomass equation dataset based on an extensive literature survey that covered broad geographical, climatic and forest vegetation gradients across China. Our dataset represents a major expansion in comparison to the biomass equation datasets currently available for China (Chen and Zhu, 1989; Feng et al., 1999; Liang et al., 2006; Wang et al., 2005; Yuen et al., 2016; Zhang et al., 2013) and thus fills an important regional gap relevant to global datasets (Henry et al., 2015). Our dataset also lays a solid data foundation for the estimation of forest biomass and carbon and provides general laws for plant allometric scaling. Moreover, this work highlights five limitations and identifies the potential for future biomass equation research in China, as follows.
-
There are still major gaps, and new equations, particularly for natural forests and most noncommercial tree species, are needed.
-
To some extent, transparent and consistent protocols for tree biomass measurements, especially for the belowground sector, were lacking in some studies. Moreover, belowground biomass was not measured or was measured inadequately in many studies.
-
Component-based biomass equations were always fitted without paying much attention to the additivity of biomass component equations in practice. To date, various model specification and parameter estimation methods have been proposed to ensure additivity, such as by performing seemly unrelated regression (Dong et al., 2015).
-
The complete reports on biomass equations should cover the regression method, sample size, equation evaluation (e.g., R2, error estimates of equations, standard errors of equation coefficients and correction factors for log-linearized equations) and applicable ranges. However, these reports are often incomplete in current studies, largely due to the lack of uniform reporting standards.
-
Limited sample trees with relatively narrow ranges of tree diameter and height were selected from small biotic (e.g., stand age and tree species) and abiotic (e.g., climate and soil) gradients. Additionally, large trees were often ignored in sampling campaigns. These disadvantages limit the applicability of the biomass equations. To overcome these drawbacks, further research is required to evaluate the quality and performance of these equations and develop generalized biomass equations over broader ranges of abiotic and biotic conditions.
Table A1Categorization of age class by dominant tree species, growing region and stand origin1.
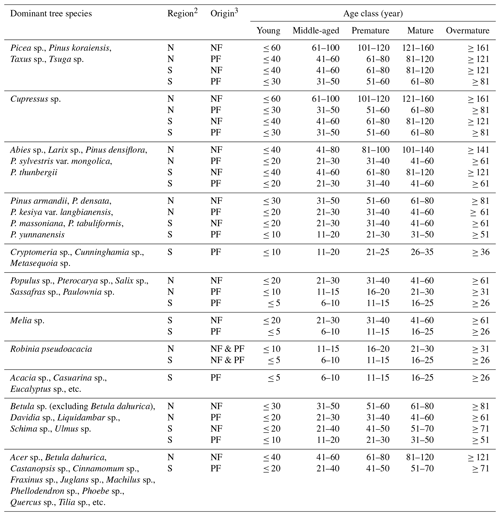
1 National Forestry and Grassland Administration of China: Regulations for Age-class and Age-group Division of Main Tree Species (LY/T 2908-2017), National Forestry and Grassland Administration of China, Beijing, China, 10 pp., 2017. 2 Mainland China is categorized by a demarcation line (Qinling Mountains–Huai River Line) into two regions: the north (N, the north of the line, including cold and warm-temperate zones) and the south (S, the south of the line, including subtropical and tropical zones). 3 Forests are categorized by stand origin into natural forest (NF) and planted forest (PF).
Table B1Height–diameter curves for China's tree species (group)1.
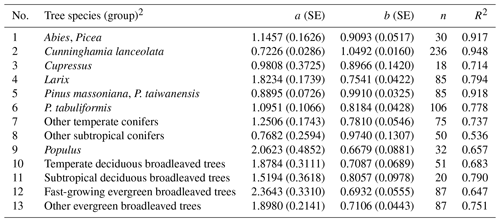
1 Data of mean diameter at breast height (D, cm) and height (H, m) are from Luo et al. (2013). H−D curves are depicted by using model , where a and b are equation coefficients. SE, standard error; n, sample size; and R2, coefficient of determination. 2 To categorize tree species (group), the following factors are considered in decreasing order of significance: adequate sample size (generally > 20), similar phylogenetic relationship, similar ecophysiological characteristics and similar growth conditions.
Table D1Number of compiled biomass equations by tree species and biomass component. “–” denotes no equations for a tree biomass component (group). Species names are checked with online Flora of China (http://frps.iplant.cn/, last access: 1 November 2019). Mixed forest in the “tree species” column refer to tree species pooled (e.g., deciduous broadleaved trees, a certain diameter-class mixed species, even generalized) that equations are developed for. Abbreviations: SBs, stem biomass subcomponents (stem wood and bark); SB, stem biomass; BBs, branch biomass subcomponents (e.g., different aged branches); BB, branch biomass; LBs, leaf biomass subcomponents (different aged leaves); LB, leaf biomass; FF, flower and fruit biomass; CB, tree crown biomass (BB + LB); AW, aboveground woody biomass (SB + BB); AG, aboveground biomass (SB + BB + LB + FF); BGs, belowground biomass subcomponents (e.g., different diameter roots); BG, belowground biomass; TB, tree biomass (AG + BG).

XW, ZO and YL originated, conceived and designed the work. YL, XW and FL developed and analyzed the equation dataset. All authors contributed to the writing of the manuscript.
The authors declare that they have no conflict of interest.
We would like to thank Yang Xiao and Jianhua Zhu for their short comments on a previous version of the paper.
This research has been supported by the National Natural Science Foundation of China (grant no. 31500388), the National Key R&D Program of China (grant no. 2018YFC0507303), the Open Foundation of State Key Laboratory of Urban and Regional Ecology of China (grant no. SKLURE 2016-2-3), and the China Postdoctoral Science Foundation (grant nos. 2016M601144 and 2017T100112).
This paper was edited by Birgit Heim and reviewed by one anonymous referee.
Anitha, K., Verchot, L. V., Joseph, S., Herold, M., Manuri, S., and Avitabile, V.: A review of forest and tree plantation biomass equations in Indonesia, Ann. Forest Sci., 72, 981–997, 2015.
Baskerville, G. L.: Use of logarithmic regression in the estimation of plant biomass, Can. J. Forest Res., 2, 49–53, 1972.
Bustamante, M., Robledo-Abad, C., Harper, R., Mbow, C., Ravindranat, N. H., Sperling, F., Haberl, H., Pinto, A. D. S., and Smith, P.: Co-benefits, trade-offs, barriers and policies for greenhouse gas mitigation in the agriculture, forestry and other land use (AFOLU) sector, Global Change Biol., 20, 3270–3290, 2014.
Chave, J., Réjou-Méchain, M., Búrquez, A., Chidumayo, E., Colgan, M. S., Delitti, W. B. C., Duque, A., Eid, T., Fearnside, P. M., Goodman, R. C., Henry, M., Martínez-Yrízar, A., Mugasha, W. A., Muller-Landau, H. C., Mencuccini, M., Nelson, B. W., Ngomanda, A., Nogueira, E. M., Ortiz-Malavassi, E., Pélissier, R., Ploton, P., Ryan, C. M., Saldarriaga, J. G., and Vieilledent, G.: Improved allometric models to estimate the aboveground biomass of tropical trees, Global Change Biol., 20, 3177–3190, 2014.
Chen, C. G. and Zhu, J. F.: Manual on Biomass Equations of Major Tree Species in Northeast China, China Forestry Publishing House, Beijing, China, 1989 (in Chinese).
Cheng, Z., Gamarra, J. G. P., and Birigazzi, L.: Inventory of Allometric Equations for Estimating Tree Biomass: A Database for China, MRV Report 18, UN-REDD Programme, Rome, Italy, 17 pp., 2014.
Clifford, D., Cressie, N., England, J. R., Roxburgh, S. H., and Paul, K. I.: Correction factors for unbiased, efficient estimation and prediction of biomass from log-log allometric models, Forest Ecol. Manag., 310, 375–381, 2013.
Dong, L. H., Zhang, L. J., and Li, F. R.: Developing additive systems of biomass equations for none hardwood species in Northeast China, Trees, 29, 1149–1163, 2015.
Eamus, D., McGuinness, K., and Burrows, W.: Review of Allometric Relationships for Estimating Woody Biomass for Queensland, the Northern Territory and Western Australia, Technical Report No. 5a, National Carbon Accounting System, Canberra, Australia, 56 pp., 2000.
Fang, J. Y., Shen, Z. H., Tang, Z. Y., Wang, X. P., Wang, Z. H., Feng, J. M., Liu, Y. N., Qiao, X. J., Wu, X. P., and Zheng, C. Y.: Forest community survey and the structural characteristics of forests in China, Ecography, 35, 1059–1071, 2012.
FAO (Food and Agriculture Organization of United Nations): Global Forest Resources Assessment 2015, FAO, Rome, 44 pp., 2016.
Feng, Z. W., Wang, X. K., and Wu, G.: Biomass and Productivity of Forest Ecosystems in China, Science Press, Beijing, China, 241 pp., 1999 (in Chinese).
Finér, L., Ohashi, M., Noguchi, K., and Hirano, Y.: Factors causing variation in fine root biomass in forest ecosystems, Forest Ecol. Manag., 261, 265–277, 2011.
Forrester, D. I., Tachauer, I. H. H., Annighoefer, P., Barbeito, I., Pretzsch, H., Ruiz-Peinado, R., Stark, H., Vacchiano, G., Zlatanov, T., Chakraborty, T., Saha, S., and Sileshi, G. W.: Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate, Forest Ecol. Manag., 396, 160–175, 2017.
Henry, M., Picard, N., Trotta, C., Manlay, R. J., Valentini, R., Bernoux, M., and Saint-André, L.: Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations, Silva Fenn., 45, 477–569, 2011.
Henry, M., Jara, M. C., Réjou-Méchain, M., Piotto, D., Fuentes, J. M. M., Wayson, C., Guier, F. A., Lombis, H. C., López, E. C., Lara, R. C., Rojas, K. C., Pasquel, J. D. A., Montoya, Á. D., Vega, J. F., Galo, A. J., López, O. R., Marklund, L. G., Cahidez, J. J. N., Malavassi, E. O., Pérez, J., Zea, C. R., García, L. R., Pons, R. R., Sanquetta, C., Scott, C., Westfall, J., Zapata-Cuartas, M., and Saint-André, L.: Recommendations for the use of tree models to estimate national forest biomass and assess their uncertainty, Ann. Forest Sci., 72, 769–777, 2015.
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G., and Jarvis, A.: Very high resolution interpolated climate surfaces for global land areas, Int. J. Climatol., 25, 1965–1978, 2005.
Jenkins, J. C., Chojnacky, D. C., Heath, L. S., and Birdsey, R. A.: National-scale biomass estimators for United States tree species, Forest Sci., 49, 12–35, 2003.
Jenkins, J. C., Chojnacky, D. C., Heath, L. S., and Birdsey, R. A.: Comprehensive Database of Diameter-based Biomass Regressions for North American Tree Species, General Technical Report NE-319, Northeastern Research Station, Forest Service, Department of Agriculture, United States, 45 pp., 2004.
Jucker, T., Caspersen, J., Chave, J., Antin, C., Barbier, N., Bongers, F., Dalponte, M., van Ewijk, K. Y., Forrester, D. I., Haeni, M., Higgins, S. I., Holdaway, R. J., Iida, Y., Lorimer, C., Marshall, P. L., Momo, S., Moncrieff, G. R., Ploton, P., Poorter, L., Rahman, K. A., Schlund, M., Sonké, B., Sterck, F. J., Trugman, A. T., Usoltsev, V. A., Vanderwel, M. C., Waldner, P., Wedeux, B. M. M., Wirth, C., Wöll, H., Woods, M., Xiang, W., Zimmermann, N. E., and Coomes, D. A.: Allometric equations for integrating remote sensing imagery into forest monitoring programmes, Global Change Biol., 23, 177–190, 2017.
Keith, H., Barrett, D., and Keenan, R.: Review of Allometric Relationships for Estimating Woody Biomass for New South Wales, the Australian Capital Territory, Victoria, Tasmania and South Australia, Technical Report No. 5b, National Carbon Accounting System, Canberra, Australia, 111 pp., 2000.
Liang, W. J., Hu, H. Q., Liu, F. J., and Zhang, D. M.: Research advance of biomass and carbon storage of poplar in China, J. Forestry Res., 17, 75–79, 2006.
Luo, Y. J., Wang, X. K., Zhang, X. Q., and Lu, F.: Biomass and Its Allocation of Forest Ecosystems in China, China Forestry Publishing House, Beijing, China, 332 pp., 2013 (in Chinese).
Luo, Y. J., Zhang, X. Q., Wang, X. K., and Lu, F.: Biomass and its allocation of Chinese forest ecosystems, Ecology, 95, 2026–2026, 2014.
Luo, Y. J., Wang, X. K., and Ouyang, Z. Y.: A China's normalized tree biomass equation dataset, PANGAEA, https://doi.org/10.1594/PANGAEA.895244, 2018.
Mokany, K., Raison, R. J., and Prokushkin, A. S.: Critical analysis of root:shoot ratios in terrestrial biomes, Global Change Biol., 12, 84–96, 2006.
National Forestry and Grassland Administration of China: Regulations for Age-class and Age-group Division of Main Tree Species (LY/T 2908-2017), National Forestry and Grassland Administration of China, Beijing, China, 10 pp., 2017 (in Chinese).
Návar, J.: Biomass component equations for Latin American species and groups of species, Ann. Forest Sci., 66, 208–208, 2009.
Pan, W. C., Li, L. C., Gao, Z. H., Zhang, X. Q., and Tang, D. Y.: The biomass and productivity of Chinese fir plantations, Hunan Forestry Sci. Technol., 5, 1–12, 1978 (in Chinese).
Pan, Y., Birdsey, R. A., Phillips, O. L., and Jackson, R. B.: The structure, distribution, and biomass of the world's forests, Annu. Rev. Ecol. Evol. Syst., 44, 593–622, 2013.
Paul, K. I., Roxburgh, S. H., Chave, J., England, J. R., Zerihun, A., Specht, A., Lewis, T., Bennett, L. T., Baker, T. G., Adams, M. A., Huxtable, D., Montagu, K. D., Falster, D. S., Feller, M., Sochacki, S., Ritson, P., Bastin, G., Bartle, J., Wildy, D., Hobbs, T., Larmour, J., Waterworth, R., Stewart, H. T. L., Jonson, J., Forrester, D. I., Applegate, G., Mendham, D., Bradford, M., O'Grady, A., Green, D., Sudmeyer, R., Rance, S. J., Turner, J., Barton, C., Wenk, E. H., Grove, T., Attiwill, P. M., Pinkard, E., Butler, D., Brooksbank, K., Spencer, B., Snowdon, P., O'Brien, N., Battaglia, M., Cameron, D. M., Hamilton, S., McAuthur, G., and Sinclair, J.: Testing the generality of above-ground biomass allometry across plant functional types at the continent scale, Global Change Biol., 22, 2106–2124, 2016.
Pilli, R., Anfodillo, T., and Carrer, M.: Towards a functional and simplified allometry for estimating forest biomass, Forest Ecol. Manag., 237, 583–593, 2006.
Rojas-García, F., De Jong, B. H. J., Martínez-Zurimendí, P., and Paz-Pellat, F.: Database of 478 allometric equations to estimate biomass for Mexican trees and forests, Ann. Forest Sci., 72, 835–864, 2015.
Snowdon, P.: A ratio estimator for bias correction in logarithmic regressions, Can. J. Forest Res., 21, 720–724, 1991.
Ter-Mikaelian, M. T. and Korzukhin, M. D.: Biomass equations for sixty-five North American tree species, Forest Ecol. Manag., 97, 1–24, 1997.
Wang, W. J., Zu, Y. G., Wang, H. M., Matsuura, Y., Sasa, K., and Koike, T.: Plant biomass and productivity of Larix gmelinii forest ecosystem in northeast China: Intra- and inter-species comparison, Eurasian J. Forest Res., 8, 21–41, 2005.
Whittaker, R. H.: Communities and Ecosystems, 2nd edn., Macmillan, New York, 385 pp., 1975.
Xiang, W. H., Liu, S. H., Deng, X. W., Shen, A. H., Lei, X. D., Tian, D. L., Zhao, M. F., and Peng, C. H.: General allometric equations and biomass allocation of Pinus massoniana trees on a regional scale in southern China, Ecol. Res., 26, 697–711, 2011.
Yuen, J. Q., Fung, T., and Ziegler, A. D.: Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above- and below-ground carbon estimates, Forest Ecol. Manag., 360, 323–340, 2016.
Zhang, X. S.: Vegetation Map of China and Its Geographic Patterns, Geological Publishing House, Beijing, China, 91–124, 2007 (in Chinese).
Zhang, X. Q., Duan, A. G., and Zhang, J. G.: Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method, PLoS ONE, 8, e79868, https://doi.org/10.1371/journal.pone.0079868, 2013.
Zhang, J. W. and Feng, Z. W.: Relationships between planting density and the biomass of Chinese fir plantations in hilly region of Taoyuan County, Hunan Forest Sci. Technol., 5, 1–6, 1979.
Zianis, D., Muukkonen, P., Mäkipää, R., and Mencuccini, M.: Biomass and stem volume equations for tree species in Europe, Silva Fenn., 4, 1–63, 2005.